第二章 各种各样的数学

大多数图形只是将数学公式直接转为代码。因此，数学公式越简洁，最后转换出来的代码越简洁明了；这本书的大部分内容都集中在使用正确的数学公式来完成这项工作。本章将回顾高中和大学中所学的数学知识，因此本章可以视为是一份参考，而不是一份教程。它其实就是一个数学大杂烩，选择每一个小节是因为它们在“标准”的数学课程中有点不同寻常，也因为它们在图形学中很重要，并且通常不是从几何学的角度来处理。本章除了建立对本书中所使用的数学符号的回顾，还强调了在标准大学本科课程中跳过的一些知识点，例如：三角形中的质心坐标。并且本章不会严格证明这些数学知识，更多的强调直觉和几何解释。关于线性代数的讨论推迟到第 5 章，放在第 6 章变换矩阵之前。我们鼓励读者浏览本章熟悉涉及到的知识点，并且在需要的时候回顾它们。章末的练习题能够帮助读者审查自对知识点的熟悉程度，从而回顾的对应的知识点。

2.1 集合和映射

映射(Mappings)，也称为函数(Functions)，是数学和编程的基础。如同编程中的函数，数学中的映射会接受一种类型的入参，然后映射到(返回)特定类型的对象。编程中我们提到的“类型”，在数学中被定义为集合(set)。若一个对象是某个集合中的元素，我们使用符号 ∈ 来表示这种关系。例如：a ∈ S，可以被解读为“a 是集合 S 中的一个元素”。给定任意两个集合A和B，可以通过求它们的笛卡尔积(Cartesian product)得到第三个集合，记为：A × B。集合 A x B 是由所有可能的有序对$(a,b)$ 组成，其中a ∈ A，b ∈ B。为了简写，可以使用符号$A^2$表示集合A × A。我们可以扩展笛卡尔积，从三个集合中创建所有可能的有序三元组，以此类推，更多的集合可以创建不同的有序元组。

常用的集合包括

• $R$: 实数集
• $R^+$: 正实数(包括 0)
• $R^2$: 二维平面上的一个有序对
• $R^n$: n 维笛卡尔空间中的点
• $Z$: 整数
• $S^2$: 单位球面上的三维点的集合($R^3$中的点)

记住，虽然$S^2$是由嵌入三维空间的点组成的，但它们是在一个可以用两个变量进行参数化的曲面上，所以可以把它看作是一个二维集合。映射的表示方式采用箭头和冒号，例如：$f: R \mapsto Z$。你可以看作“有一个函数 f，接受一个实数作为入参且映射到了一个整数上面。”箭头左边的集合称为该函数的域，箭头右边则称为函数的目标。程序员可能更容易这么理解：“有一个函数 f，入参是一个实数，函数返回一个整数。”换句话说，上述集合的表示形式等价于一般程序的表示形式：$integer f(real) \gets equivalent \to f: R \mapsto Z$。因此，冒号箭头的形式可以简单看出是程序语法。

点$f(a)$称为 a 的映像，集合A(a 的值域子集)的映像是包含A 中所有点的映像的子集。整个值域的映像称为函数的范围。

2.1.1 逆映射

如果存在一个函数$f: A \mapsto B$，同时可能存在一个逆函数$f^{-1}: B \mapsto A$，这是由$f^{-1}(b) = a$ 定义，其中$b = f(a)$。该定义成立当且仅当每一个b ∈ B是函数$f$下某个点映像（即值域等于目标），并且只存在一个这样的点（即$f(a) = b$只能找到唯一一个$a$满足）。像这种映射或函数被称为“双射”（bijections）。双射将每一个a ∈ A映射到唯一的b ∈ B上，对于每一个b ∈ B，存在一个特定的a ∈ A使得$f(a) = b$。如图：

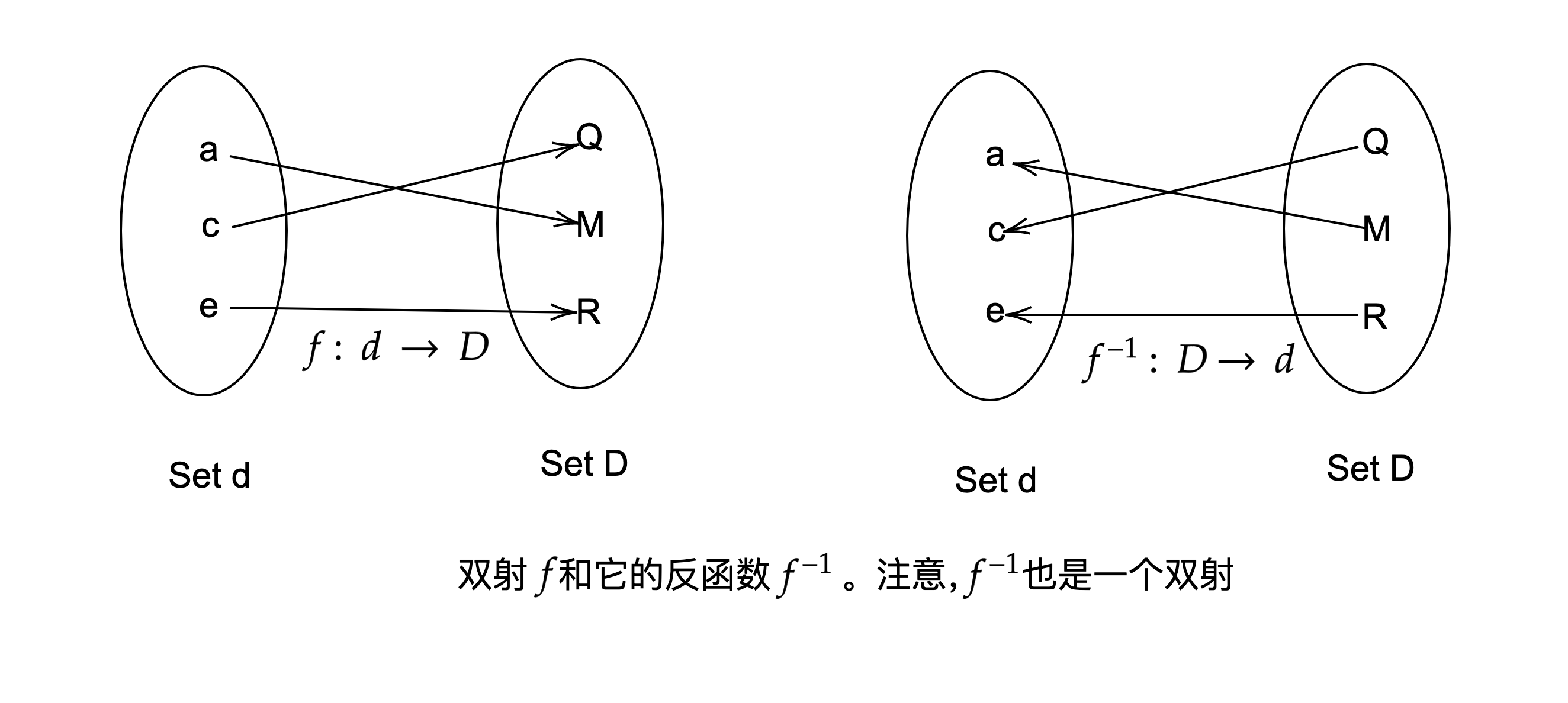用骑手和马来举例，他们之间的双射可以表示为每一个骑手都会骑一匹马，而每一匹马都被骑手骑。相关的函数为骑手(马)和马(骑手)，它们之间互为逆函数。若函数不是双射，则没有逆函数。如图：

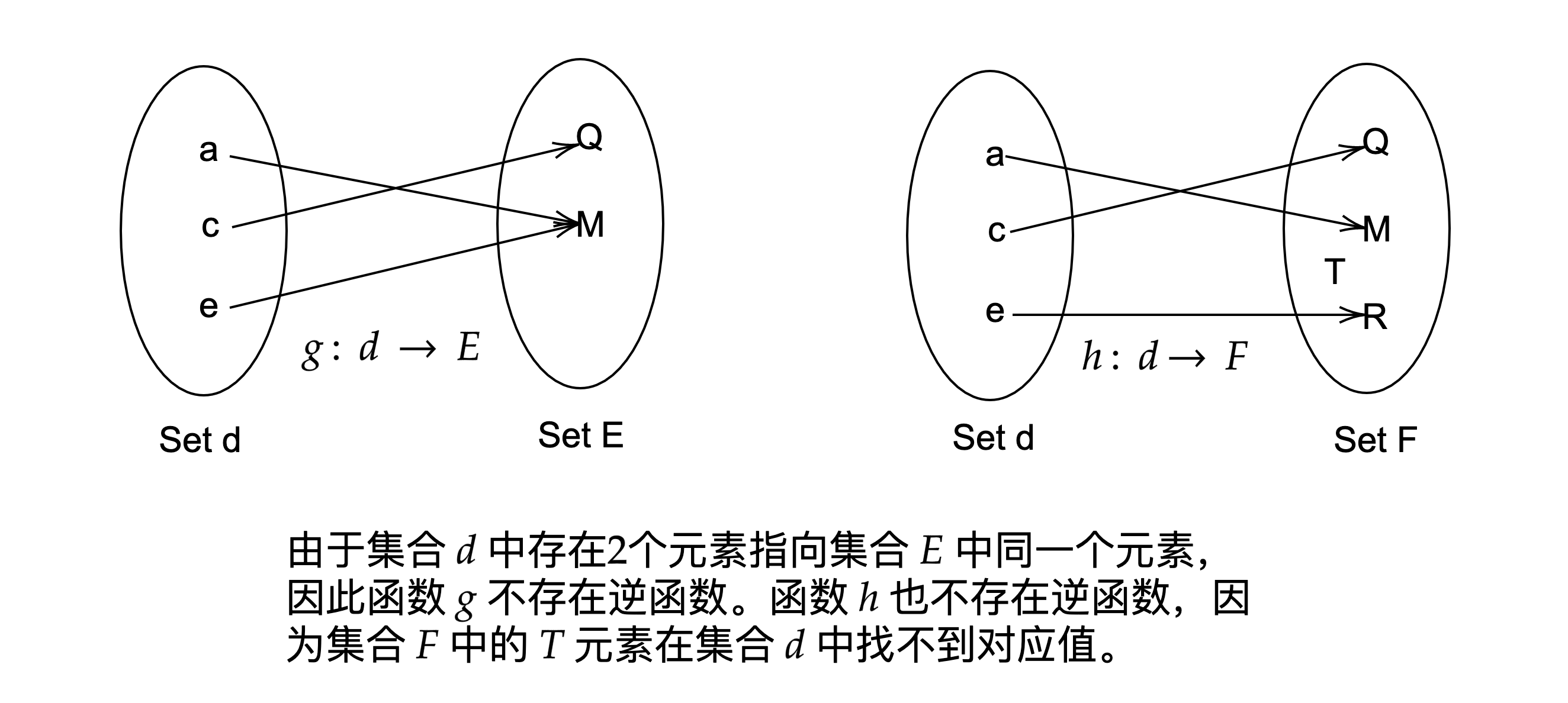一个双射函数的例子：$f: R \mapsto R$，满足$f(x) = x^3$。它的逆函数是$f^{-1}(x) = \sqrt[3]x$。这个例子表明，标准表示法可能有些笨拙，因为$x$在$f$和f^{−1}中都被用作伪变量。有时候为了更加直观，可以使用不同的伪变量，比如，$y = f(x)$和$x = f^{-1}(y)$。因此，上面的例子可以表示为$y = x^3$和$x = \sqrt[3]y$。再举一个非双射函数的例子：$f: R \mapsto R$，满足$sqr(x) = x^2$。两点原因：1.$x^2 = (-x)^2$;2.值域中不存在目标的负数部分。注意：当我们限制值域为$R^+$时，可以定义一个逆函数，这时，$\sqrt{x}$是一个有效的逆函数。